Monet sparsity optimization

In Spring 2025, EleutherAI was working on replacing layers in pretrained transformers with sparse transcoders(1, 2). We could finetune transcoders to match or even improve on the models on crossentropy, but we needed to make the MLPs so wide that inference was impractical.

"Product Key Memory Sparse Coders" was one of our attempts to improve transcoder efficiency. The main bottleneck in transcoder inference is the encoder forward pass. We need to compute the outputs of a very wide MLP, usually an OOM wider than a usual MLP encoder. We considered various ways to decompose the weights to speed up the forward pass, but they rarely yielded a Pareto improvement. We have not considered ideas like quantized training, only focusing on the architecture.

One MLP architecture we considered was Monet. This architecture was used by the authors for from-scratch pretraining, and not replacing individual layers like in our experiments. Monet is closer to an MoE than a sparse coder. It has a very large (262k) number of small (~12 hidden dimension) experts, and the weights of each are compressed using one of two schemes (Section 3).

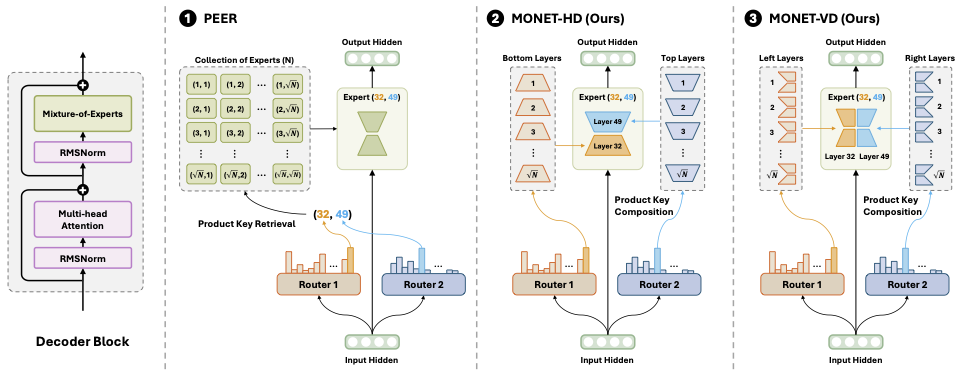
The basic idea behind them is to divmod the expert index by the square root of the index count and use the two indices to find pieces of the weights used for inference. This strategy is inspired by product key memories, but is not a direct port like our PKM sparse coders were. There is a router every 4 layers, and it is also decomposed with PKM, meaning. Monet achieves comparable accuracy to a dense model of the same size and has interpretable features¹ by default.

An implementation of the Monet MLP can be found in the official Github repo. The core forward pass of a vertically decomposed Monet is as follows:

def vanilla_forward(
   self, x: torch.Tensor, g1: torch.Tensor, g2: torch.Tensor
) -> torch.Tensor:
   # x: b, t, d_in
   # g1, g2: b, t, moe_heads, moe_experts
   g1, g2 = g1.type_as(x), g2.type_as(x)
   x1 = self.act_fn(self.u1(x).unflatten(-1, (self.config.moe_experts, -1)))
   x2 = self.act_fn(self.u2(x).unflatten(-1, (self.config.moe_experts, -1)))
   # x1, x2: b, t, moe_experts, moe_dim // 2
   # each represents half of the hidden dimension of the MLP


   x11 = self.v11(torch.einsum("btim,bthi->btim", x1, g1).flatten(-2))
   x12 = self.v12(torch.einsum("btjm,bthj,bthi->btim", x2, g2, g1).flatten(-2))
   x13 = torch.einsum("bthi,id->btd", g1, self.b1.type_as(x))


   x22 = self.v22(torch.einsum("btjm,bthj->btjm", x2, g2).flatten(-2))
   x21 = self.v21(torch.einsum("btim,bthi,bthj->btjm", x1, g1, g2).flatten(-2))
   x23 = torch.einsum("bthj,jd->btd", g2, self.b2.type_as(x))


   # x11, x12, x13, x21, x22, x23: b, t, d_in // 2
   # x11/x22: result of a forward pass through a single chosen half-MLP
   # x12/x21: results from passing a half-MLP’s post-activations into another half-MLP
   # x13/x23: contributions from the biases of the chosen half-MLPs


   return torch.cat((x11 + x12 + x13, x21 + x22 + x23), dim=-1)

Notice that this implementation doesn't make use of the sparsity of the picked experts. I benchmarked this implementation against other language models:

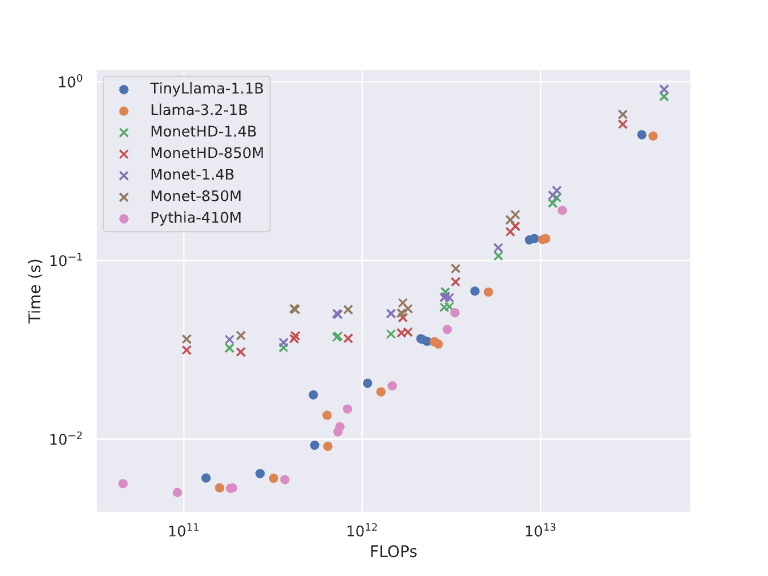
This shows that the model is implemented efficiently for the amount of FLOPs it uses when the batch size is high enough. Of course, these numbers count all sparse operations as dense ones and thus overestimate the number of operations a sparse implementation would need to perform. For all Monet sizes, a FLOP reduction of 30x or more is achievable for the MLP operations if sparsity is taken advantage of fully and the TopK operation is sped up.

All three of the Monet MLP operations can be rewritten to take advantage of the sparsity. I tried optimizing the bias and the same-half affine operations using the sparse matmul kernel (Gao et al. 2024, DenseSparseMatmul), and it did not improve MLP forward pass time at 1.4B. Another obstacle to using sparse kernels is that it also requires us to know the indices of the active elements, which requires an expensive TopK operation. The original Monet paper avoided it by approximating the TopK threshold using the Normal CDF and setting values below the threshold to 0 without selecting their indices. A change that would make any optimization viable in the first place is changing the from thresholded TopK to Maxout:

def groupmax(x, k):
   x = x.unflatten(-1, (k, -1))
   v, i = x.max(dim=-1)
   i = i + torch.arange(0, k, device=i.device, dtype=i.dtype) * x.shape[-1]
   return v, i

We don’t know if this change preserves language modelling performance, but would expect it to, as Maxout works similarly to TopK for sparse coders. Testing this would require retraining the model.

With this change, the cross-half part of the forward pass can be slightly sped up by considering only the active indices in the tensor contraction:

def sparse_g1_g2(
   x1, g1_i, g1_v, g2_i, g2_v, v21
):
   g1_index = g1_i[..., None].expand(-1, -1, -1, -1, x1.shape[-1]).flatten(-3, -2)
   pre_g1_g2 = torch.gather(x1, -2, g1_index).view(*g1_i.shape, x1.shape[-1])
   post_g1_g2_ = torch.einsum("bthkm,bthk,bthl->bthlm", pre_g1_g2, g1_v, g2_v,)
   post_g1_g2 = torch.zeros((
       *x.shape[:2], g2.shape[-1], x1.shape[-1]
   ), device=x.device, dtype=x.dtype)
   post_g1_g2_ = post_g1_g2_.flatten(-3, -2)
   post_g1_g2.scatter_add_(-2, g2_i.flatten(-2)[..., None].expand(-1, -1, -1, x1.shape[-1]), post_g1_g2_)
   post_g1_g2 = post_g1_g2.flatten(-2)
   x21 = v21(post_g1_g2)
   return x21

Where g1_i/g1_v (and g2_i/g2_v) are the indices and values of the top K elements of g1 and g2 for each head (shape B x T x moe_heads x moe_experts).

This speeds up a forward pass on 2^16 tokens with Monet-VD-850M from 46ms to 35ms; with 1.4B from 62.3ms to 54.8ms; on 3*2^14 tokens with 4.1B from 90ms to 80ms. The speedup seems to stabilize at around 12% for large models.

These tests were run on 1 A40 GPU. We briefly tested if a CPU implementation could see an improvement, but found that there was no benefit over an AVX2 dense matrix multiplication on AMD EPYC 7B12 at the current levels of sparsity.

Thus Monet joins the list of architectures that have a clever sparsity trick but don't see performance improvements from it.

v11_flops_full = moe_experts * moe_dim * moe_heads + moe_experts * moe_dim * d_out
v11_flops_compressed = moe_k * moe_dim * moe_heads + moe_k * moe_dim * d_out
v12_flops_full = moe_dim * moe_heads * moe_experts + moe_dim * moe_heads * moe_experts + moe_experts * moe_dim * d_out
v12_flops_compressed = moe_dim * moe_heads * moe_k + moe_dim * moe_heads * moe_experts + moe_k * moe_dim * d_out
v13_flops_full = moe_experts * d_out
v13_flops_compressed = moe_k * d_out
flops_full = v12_flops_full + v11_flops_full + v13_flops_full
flops_compressed = v12_flops_compressed + v11_flops_compressed + v13_flops_compressed

This ratio is 64 for the 850M model (leading to ~57.273 estimated FLOPs ratio).